GARIS SUDUT DAN CONTOH SOAL SERTA PEMBAHASANNYA
Mei 03, 2017
Add Comment
Dalam matematika kita mengenal istilah sudut. Sudut adalah suatu daerah yang dibentuk oleh dua buah ruas garis yang titik pangkalnya sama. Sudut dibedakan menjadi beberapa jenis yaitu sudut tumpul, sudut lancip, sudut lurus, sudut siku-siku, sudut refleks, dan sudut satu putaran penuh.
Secara umum, ada dua satuan dalam pengukuran sudut, yaitu satuan derajat (o) dan satuan radian (rad). Kita ketahui bahwa satu putaran penuh dengan arah perputaran berlawanan jarum jam adalah 360o. Dengan demikian jika busur lingkaran kita bagi menjadi 360 bagian yang sama, maka besarnya tiap sudut pusat yang terjadi adalah 1o.
Untuk kepentingan ketelitian pengukuran suatu sudut, maka satuan derajat dibagi menjadi 60 bagian yang sama dan disebut menit. Sedangkan setiap menit dibagi lagi menjadi 60 bagian yang sama dan disebut detik. Simbol (‘) dan (“) berturut-turut digunakan untuk menyatakan ukuran sudut dalam satuan menit dan detik.
Konversi Satuan Sudut1° = 60′ → (1 derajat = 60 menit)
1′ = 60″ → (1 menit = 60 detik)
1° = 3600″ → (1 derajat = 3600 detik)
Sudut-Sudut Penting
Sudut siku-siku → 90°
Sudut lurus → 180°
Sudut lancip → antara 0° dan 90°
Sudut tumpul → antara 90° dan 180°
Satu lingkaran penuh adalah 360°
Hubungan Sudut-Sudut
Suplemen → Berpelurus (membentuk sudut 180°)
Komplemen →Berpenyiku (membentuk sudut 90°)
Bertolak Belakang → Dua sudut yang bertolak belakang sama besar
Contoh Soal 1
Perhatikan gambar di bawah ini
Besar ∠ABD adalah ….
A. 98°
B. 105°
C. 112°
D. 119°
(UN 2008/2009)
Penyelesaian:
Untuk menjawab soal ini hal pertama yang Anda cari adalah nilai x. Dalam hal ini ∠ABD dan ∠CBD merupakan sudut saling pelurus, maka:
∠ABD + ∠CBD = 180°
7x° + 5x° = 180°
12x° = 180°
x = 15°
∠ABD = 7x°
∠ABD = 7. 15°
∠ABD = 105°
Jadi, besar ∠ABD adalah 105° (Jawaban B)
Contoh Soal 2
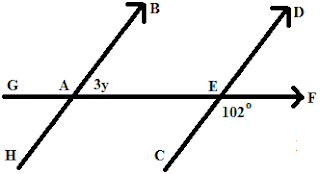
Perhatikan gambar di bawah ini
Nilai y adalah ….
A. 24°
B. 25°
C. 26°
D. 34°
(UN 2008/2009)
Penyelesaian:
Untuk menjawab soal ini Anda harus paham konsep hubungan antarsudut jika dua garis sejajar dipotong oleh garis lain. Dalam hal ini ∠CEF dan ∠EAH merupakan sudut sehadap, maka:
∠EAH = ∠CEF
∠EAH = 102°
∠EAH + ∠BAE = 180° (sudut saling berpelurus)
102°+ 3y = 180°
3y = 180° - 102°
3y = 78°
y = 26° (Jawaban B)
Contoh Soal 3
Perhatikan gambar di bawah ini
Besar pelurus sudut SQR adalah ….
A. 101°
B. 100°
C. 95°
D. 92°
(UN 2012/2013 paket 54)
Penyelesaian:
Perhatian** soal ini merupakan soal jebakan, banyak yang mengira kalau soal tersebut menanyakan ∠SQR padahal yang diminta adalah ∠PQS. Untuk menjawab soal ini hal pertama yang Anda cari adalah nilai x. Dalam hal ini ∠PQS dan ∠SQR merupakan sudut saling pelurus, maka:
∠PQS + ∠SQR = 180°
(5x)° + (4x+9)° = 180°
9x° + 9 = 180°
9x° = 171°
x° = 19°
Pelurus ∠SQR = ∠PQS
Pelurus ∠SQR = (5x)°
Pelurus ∠SQR = (5.19)°
Pelurus ∠SQR = 95° (Jawaban C)
Contoh Soal 4
Perhatikan gambar
Besar ∠BCA adalah ….
A. 70°
B. 100°
C. 110°
D. 154°
(UN 2010/2011 paket 15)
Penyelesaian:
∠ABC + ∠CBD = 180° (saling berpelurus)
∠ABC + 112° = 180°
∠ABC = 68°
∠BCA + ∠ABC + ∠BAC = 180°
∠BCA + 68° + 42° = 180°
∠BCA + 110 = 180°
∠BCA = 70° (Jawaban A)



0 Response to " GARIS SUDUT DAN CONTOH SOAL SERTA PEMBAHASANNYA"
Posting Komentar